在行测数量关系当中,排列组合问题是一个比较常见的题型,很多考生会觉得这个部分的内容很难,一般选择直接跳过不做,但其实这个部分中也有一些可以用比较固定的思路进行求解的题型,比如隔板模型,只要掌握了这个题型的基本做题思路,就可以在这一类题型上感受到明显优势。隔板模型本质上就是解决相同元素的不同分堆问题,那什么情况下可以用“隔板法”进行求解呢?小编为大家指点迷津。
一、隔板模型的公式及应用条件:
1.公式:将n个相同的元素分给m个不同的对象,每个对象至少分到1个元素,问有多少种不同分法。此时可以运用隔板模型的求解公式进行求解,即 种。
种。
2.应用条件:
(1)所要分的元素必须完全相同
(2)所要分的元素分给不同的对象且必须全部分完,决不允许有剩余
(3)每个对象至少分到1个元素
那我们接下来看几道例题来巩固一下隔板模型求解吧。
二、例题展示:
【例1】有9台相同的电脑,分给3个学校,每个学校至少分1台电脑,共有多少种分配方案?
A.24种B.26种C.28种D.30种
【答案】C。解析:这道例题中,9台相同的电脑即所分元素相同,分给3个不同学校为分给不同的对象且全部分完,并要求每个学校至少分1台电脑即每个对象至少分到1个元素,满足隔板模型的三个条件,直接代入隔板模型的求解公式进行求解,共有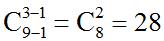 种。故本题选择C。
种。故本题选择C。
以上就是隔板模型最直接应用的考法,而隔板模型也会有一些稍微灵活的考法,比如:
【例2】有9台相同的电脑,分给3个学校,每个学校至少分2台电脑,共有多少种分配方案?
A.8种B.10种C.12种D.18种
【答案】B。解析:此题不满足隔板模型的第三个使用条件每个对象至少分到1个元素,但是可以通过转换使之满足。即想办法让第三个条件变成每个对象至少分到1个元素,此时先给每个学校分1台电脑,题目就顺利转化为剩下6台电脑,分给3个学校,每个学校至少分得一台电脑,此时就满足隔板模型的全部条件,代入隔板模型的求解公式进行求解,共有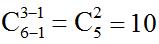 种。故本题选择B。
种。故本题选择B。
当每个对象至少分得的数量比1个多的时候,可以将多的数量提前分给这些对象,将数量转换为至少分到1个元素,再带入隔板模型的求解公式进行求解即可。
【例3】有9台相同的电脑,分给3个学校,共有多少种分配方案?
A.55种B.60种C.65种D.70种
【答案】A。解析:此题依然不满足每个对象至少分到一个的条件,要求分完即可,那么就会出现可以有学校没有分到的情况,此时同样可以想办法让每个对象至少分到1个元素,即可以让三所学校先都拥有1台电脑再进行计算,因此可以利用先借后还的方法进行转化。先从每个学校借1台电脑,此时相当于总共12台电脑,分给3所学校,每个学校至少分得一台电脑,此时就满足隔板模型的全部条件,代入隔板模型的求解公式,共有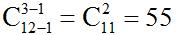 种。故本题选A。
种。故本题选A。
当每个对象至少分得的数量没有特殊要求,即随意分的情况下,可以采取先借后还的思想,向每个对象先借来1个元素,这样在进行分配时就必须还给每个对象1个元素,就转换成了每个对象至少分到1个元素,就可以代入隔板模型的求解公式进行求解。
通过以上的例题以及解析给同学们介绍了隔板模型的几种不同应用,相信同学们对隔板模型应该有了初步的认识,在后续做题的过程中若有遇到满足隔板模型的三个条件的题目,就可以直接应用公式直接进行求解,让大家在印象中的“难题”上做出自己的优势。


 种。
种。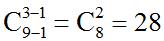 种。故本题选择C。
种。故本题选择C。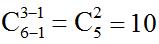 种。故本题选择B。
种。故本题选择B。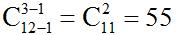 种。故本题选A。
种。故本题选A。