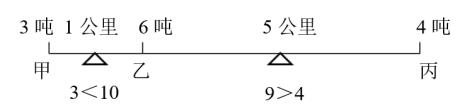行测考试当中有一个知识点,叫“货物集中问题”。一般题干会说明,直线上有多个仓库,把货物集中到一个仓库当中,研究哪个仓库的总运费最省。普通方法,计算每一个仓库的总费用来比较,会非常繁琐。而用支点法,数形结合,化抽象为形象,大大为考生争取时间优势。
一、初识题型,明晰原则
现在甲、乙两个仓库相距1公里,甲仓库有5斤面粉,乙仓库有600斤面粉,每斤面粉每公里运费0.3元,把面粉集中到哪个仓库更省运费?
A.甲仓库B.乙仓库
【解析】若集中到甲仓库,则需运600斤面粉,总运费=单价×重量×距离=0.3×600×1;若集中到乙仓库,则需运5斤面粉,总运费=0.3×5×1。我们发现单价,距离都相同,而运输重量不同,所以省钱关键在于重量,自然是运5斤比运600斤花费更少,所以选集中到乙仓库,选B。
原则:①距离不是关键,关键因素在于重量。
②把轻的货物向重的货物集中。
二、支点法巧解示范,详细步骤解读
现在直线上有三个仓库依次是甲乙丙,甲、乙两个仓库相距1公里,乙、丙仓库相距5公里。甲仓库有3吨面粉,乙仓库有6吨面粉,丙仓库有4吨面粉。每吨面粉每公里运费2元,把面粉集中到哪个仓库更省钱?
A.甲仓库B.乙仓库C.丙仓库
巧解示范:选B。用支点法(如下图)。甲乙之间设支点,3<10,乙丙之间设支点,9>4,在乙仓库前后变号,故选B。
支点法解题过程非常简洁。下面为大家阐述原理。
步骤解读:在甲乙之间的路上设支点,比较甲乙仓库哪个省运费。丙仓库可以先运到乙,再考虑留在乙还是继续集中到甲。此时,甲仓库有3吨,乙仓库共有10吨,3吨<10吨,轻的向重的运,甲向乙集中。接着,同样的操作,在乙丙之间的路上设支点,比较乙丙仓库。甲仓库可以先运到乙,此时,乙仓库共有9吨,丙仓库有4吨,9吨>4吨,轻的向重的运,丙向乙集中。我们发现在乙仓库左边小于号,右边大于号,都在说明运到乙更省钱,所以选乙仓库,选B。
方法总结:
①在路上画支点
②支点两侧总重比大小
③大小变号则得出最省仓库(轻的往重的运)
三、经典例题解析
学会支点法,解题“三步走”,一起来高效解题吧!
例题1:某电商平台每隔5千米有一座仓库,共有A、B、C、D四座仓库(如下图所示),图中数字表示各仓库库存货物的吨数。现需要把所有的货物集中存放在其中某一个仓库。如果每吨货物运输1千米需要运费3元,要使运费最小,则需将货物集中到:
A.仓库A B.仓库B C.仓库C D.仓库D
【解析】选C。用支点法(已在原图进行展示),AB之间画支点,两侧总重比大小,左侧总重10吨,右侧总重20+15+25=60吨,10<60;BC之间画支点,左侧10+20=30,右侧15+25=40,30<40;CD之间画支点,10+20+15=45,45>25。在仓库C前后发生变号,所以选C。
例题2:六个仓库,ABCDEF相邻(如下图),两个仓库之间距离均为10公里,各仓库存货量依次分别为20、25、0、35、0、15吨,每吨货物每公里运费为2元。现计划把货物全部集中在一个仓库,运费最少为多少元?
A.2800 B.2900 C.3000 D.3100
【解析】选A。用支点法(已在原图进行展示),本题仓库数比较多,我们可以猜测两端的可能性并不大,偏向于往中间集中。在CD之间画支点,左侧总重20+25=45,右侧总重35+15=50,左边往右边运,运到D;再在DE之间画支点,两侧总重分别为80和15,80>15,右边往左边运。D仓库左右变号,说明仓库最省。集中到D仓库的运费=单价×重量×距离=2×(20×30+25×20+15×20)=2800,所以选A。
支点法实在是妙,只需三步,就能快速比较出最省仓库,进而求运费只需列一个式子。而普通法却要计算多个仓库的总运费,再进行大小比较。所以仓库数越多,支点法优势越明显。支点法快快练起来吧!